ตัวเลขต่างๆ ใน FLEXIBILITY MATRIX ตามที่แสดงอยู่ในรูปนี้มีที่มาที่ไปอย่างไร

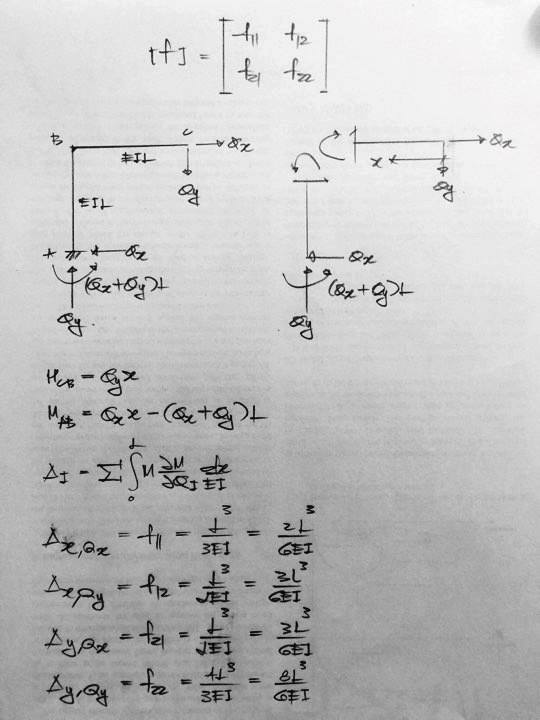
ตัวเลขต่างๆ ใน FLEXIBILITY MATRIX นี้ก็คือ DISPLACEMENT ในทิศทางใน แนวราบ และ แนวดิ่ง ที่ NODE ตรงปลายยื่น (CANTILEVER END) อันเนื่องมาจากแรง 1 หน่วย ที่กระทำทั้งใน แนวราบ และ แนวดิ่ง นั่นเองนะครับ ซึ่งจริงๆ แล้วค่า DISPLACEMENT นี้เราจะสามารถใช้วิธีการใดๆ ในการคำนวณก็ได้นะครับ ดังนั้นหากเป็นผมๆ ก็จะเลือกวิธี CLASSICAL METHOD เพราะ ผมมีความคุ้นเคยและคิดว่าวิธีการนี้จะสามารถวิเคราะห์โครงสร้างใดๆ ก็ได้อย่างตรงไปตรงมา และ ง่ายดาย ไม่จำเป็นที่จะต้องพิจารณาว่าโครงสร้างของเรานั้นมีสภาพการเซ (SWAY) หรือไม่ เราจะได้ไม่ต้องเสียเวลามาทำการสร้างสมการความสอดคล้อง (COMPATIBILTY EQUATIONS) ต่างๆ เพื่อนำมาใช้ช่วยในการวิเคราะห์โครงสร้างของเราด้วยนะครับ ซึ่งวิธีการที่ผมเลือกใช้ก็คือ CASTIGLIANO’S 2ND THEOREM นั่นเองนะครับ
ปล ในการวิเคราะห์โครงสร้างครั้งนี้ผมจะทำการตั้งสมมติฐานว่าเสาและคานของเรานั้นมีหน้าตัดมีขนาดที่ค่อนข้างใหญ่ หรือ พูดง่ายๆ คือ ผมจะไม่ทำการคิดผลของการเสียรูปอันเนื่องมาจากการเสียรูปตามแนวแกนของเสา และ คานนั่นเองนะครับ
วิธีการนี้ทำได้ง่ายๆ ครับ คือ เราทำการสร้างสมการโมเมนต์ของทุกๆ ช่วงของโครงสร้างคานและเสาของเรานะครับ ดังนั้นในโครงสร้างนี้เราจะมีสมการโมเมนต์ทั้งหมด 2 สมการนะครับ โดยหากเราจะอาศัยวิธีการ CASTIGLIANO’S 2ND THEOREM ในการวิเคราะห์โครงสร้างนี้เราก็เพียงทำการรวมผลการอินทิเกรตสมการโมเมนต์คูณกันกับผลการ PARTIAL DERIVATIVE สมการโมเมนต์ หารด้วยพจน์ที่เป็น STIFFNESS ซึ่งในที่นี้เป็น FLEXURAL STIFFNESS ซึ่งก็คือเทอม EI นะครับ โดยหากเราดูเทอมใน FLEXIBILTY MATRIX เราจะพบว่ามีทั้งหมด 4 พจน์ คือ f11 f12 f21 และ f22 โดยที่
f11 คือ การเสียรูปในทิศทางใน แนวราบ อันเนื่องมาจากแรงใน แนวราบ
f12 คือ การเสียรูปในทิศทางใน แนวราบ อันเนื่องมาจากแรงใน แนวดิ่ง
f21 คือ การเสียรูปในทิศทางใน แนวดิ่ง อันเนื่องมาจากแรงใน แนวราบ
f22 คือ การเสียรูปในทิศทางใน แนวดิ่ง อันเนื่องมาจากแรงใน แนวดิ่ง
ดังนั้นการที่เราจะหาค่าในแต่ละพจน์นั้นเราก็ต้องทำการ PARTIAL DERIVATIVE และ ทำการแทนค่าในเทอม DUMMY LOAD ให้มีค่าเท่ากับ 1 ให้มีความถูกต้องด้วยนะครับ ดังนั้น
f11 เราต้องการที่จะหาค่าการเสียรูปใน แนวราบ ดังนั้นเราต้องทำการ PARTIAL DERIVATIVE สมการโมเมนต์เทียบกันกับแรง DUMMY LOAD ใน แนวราบ และ ให้ค่าแรงใน แนวราบ เท่ากับ 1 และ แรงในแนวดิ่งเท่ากับ 0
f12 เราต้องการที่จะหาค่าการเสียรูปใน แนวราบ ดังนั้นเราต้องทำการ PARTIAL DERIVATIVE สมการโมเมนต์เทียบกันกับแรง DUMMY LOAD ใน แนวราบ และ ให้ค่าแรงใน แนวราบ เท่ากับ 0 และ แรงในแนวดิ่งเท่ากับ 1
f21 เราต้องการที่จะหาค่าการเสียรูปใน แนวดิ่ง ดังนั้นเราต้องทำการ PARTIAL DERIVATIVE สมการโมเมนต์เทียบกันกับแรง DUMMY LOAD ใน แนวดิ่ง และ ให้ค่าแรงใน แนวราบ เท่ากับ 1 และ แรงในแนวดิ่งเท่ากับ 0
f22 เราต้องการที่จะหาค่าการเสียรูปใน แนวดิ่ง ดังนั้นเราต้องทำการ PARTIAL DERIVATIVE สมการโมเมนต์เทียบกันกับแรง DUMMY LOAD ใน แนวดิ่ง และ ให้ค่าแรงใน แนวราบ เท่ากับ 0 และ แรงในแนวดิ่งเท่ากับ 1
ในเมื่อเราทำการแทนค่าต่างๆ ตามกรณ๊ที่ผมได้ให้คำแนะนำไว้ข้างต้น ทีนี้เราจะมาดูผลการวิเคราะห์โครงสร้างของเรากันบ้างนะครับ
โดยที่คำตอบของ DISPLACEMENT ในพจน์ f11 ก็คือ L^(3)/3EI = 2L^(3)/6EI ซึ่งก็จะมีค่าตรงกันกับกับค่า f11 ในหนังสือเล่มนี้นะครับ
โดยที่คำตอบของ DISPLACEMENT ในพจน์ f12 ก็คือ L^(3)/2EI = 3L^(3)/6EI ซึ่งก็จะมีค่าตรงกันกับกับค่า f12 ในหนังสือเล่มนี้นะครับ
โดยที่คำตอบของ DISPLACEMENT ในพจน์ f21 ก็คือ L^(3)/3EI = 2L^(3)/6EI ซึ่งก็จะมีค่าตรงกันกับกับค่า f21 ในหนังสือเล่มนี้นะครับ
โดยที่คำตอบของ DISPLACEMENT ในพจน์ f22 ก็คือ 4L^(3)/3EI = 8L^(3)/6EI ซึ่งก็จะมีค่าตรงกันกับกับค่า f22 ในหนังสือเล่มนี้นะครับ
จริงๆ แล้วขั้นตอนในการคำนวณนั้นก็ไม่ถือว่ายากใช่มั้ยครับ ? แต่การแก้ปัญหาในลักษณะนี้ก็จะทำให้เสียเวลาอยู่ไม่น้อยเลยทีเดียวนะครับ อย่างตอนที่ตัวผมเรียนวิชานี้ในระดับ ป โท ผมเองก็เคยพบเจอกับปัญหานี้เช่นกันนะครับ ซึ่งวิธีการที่ผมใช้ในการแก้ปัญหา คือ ผมพยายามที่จะทำการคำนวณหาค่าต่างๆ FLEXIBILITY MATRIX สำหรับกรณีโครงสร้างต่างๆ เอาไว้ล่วงหน้าตั้งแต่ยังไม่เข้าห้องสอบเลยนะครับ เวลาทำข้อสอบก็จะได้หยิบมาใช้ โดยไม่ต้องเสียเวลามานั่งทำการคำนวณในห้องสอบนั่นเองนะครับ ก็เอาเป็นว่าผมก็ขออวยพรให้น้องๆ ป โท นั้นโชคดีในการสอบในวิชา STRUCTURAL DYNAMICS กันทุกๆ คนเลยนะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
ref : https://www.facebook.com/bhumisiam/posts/1596461197066666
BSP-Bhumisiam
ผู้ผลิตรายแรก SPUN MICRO PILE
1) ได้รับมาตรฐาน มอก. มาตราฐาน397-2524 เสาเข็ม Spun Micro Pile
2) ผู้ผลิต Spun Micro Pile ที่ได้รับ Endorsed Brand รับรองคุณภาพมาตราฐาน จาก SCG
3) ผู้นำระบบ Computer ที่ทันสมัยผลิต เสาเข็ม Spun Micro Pile
4) ลิขสิทธิ์เสาเข็ม Spun Micro Pile
5) เทคโนโลยีการผลิต จากประเทศเยอรมันนี
6) ผู้ผลิต Spun Micro Pile แบบ “สี่เหลี่ยม”
7) การผลิตคอนกรีตและส่วนผสม ใช้ Program SCG-CPAC
เสาเข็ม สปันไมโครไพล์ ช่วยแก้ปัญหาได้เพราะ
1) สามารถทำงานในที่แคบได้
2) ไม่ก่อให้เกิดมลภาวะทางเสียง
3) หน้างานสะอาด ไม่มีดินโคลน
4) สามารถรับน้ำหนักได้ 20-40 ตัน/ต้น
5) สามารถตอกชิดกำแพง ไม่ก่อให้โครงสร้างเดิมเสียหาย
สนใจติดต่อสินค้า เสาเข็ม ไมโครไพล์ (Micropile)
สปันไมโครไพล์ (Spun MicroPile) มาตรฐาน มอก.
ติดต่อ สายด่วน โทร :
081-634-6586
082-790-1447
082-790-1448
082-790-1449
ID LINE :
LINE ID1 = bhumisiam
LINE ID2 = 0827901447
LINE ID3 = 0827901448
LINE ID4 = bsp15
บริษัท ภูมิสยาม ซัพพลาย จำกัด
http://www.ไมโครไพล์.com
#Micropile
#SpunMicropile
#ไมโครไพล์
#สปันไมโครไพล์
#เสาเข็มไมโครไพล์
#เสาเข็มสปันไมโครไพล์