สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
กลับมาพบกันในทุกๆ วันเสาร์แบบนี้อีกครั้งหนึ่งซึ่งผมก็จะมาพบกับเพื่อนๆ เพื่อที่จะพูดคุยกันถึงหัวข้อ “ถาม-ตอบชวนสนุก” กันนะครับ
โดยที่ในวันนี้ประเด็นที่ผมได้เลือกนำเอามาตั้งเป็นคำถามประจำสัปดาห์นั้นจะมีความเกี่ยวข้องกันกับเรื่อง ความรู้ดีๆ สำหรับนักเรียนและนักศึกษาที่ผมได้ทำการโพสต์ถึงในสัปดาห์ที่ผ่านมาและก็เหมือนเช่นเคยผมคงจะต้องออกตัวอีกครั้งหนึ่งว่า คำถามประจำสัปดาห์นี้สุดแสนจะง่ายมากๆๆๆๆๆๆๆๆๆ โดยที่โจทย์ในวันนี้ก็คือ

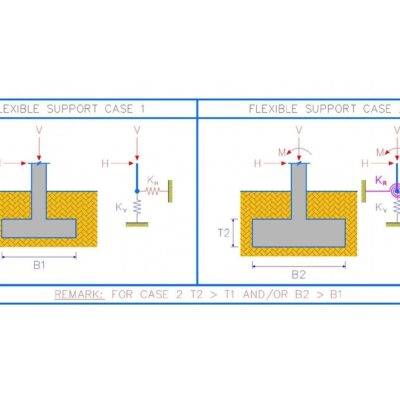
จากในรูปจะเป็นโครงสร้างโครงข้อแข็งที่มีลักษณะเป็น STATICALLY INDTERMINATE ซึ่งจะประกอบไปด้วยชิ้นส่วนทั้งหมด 3 ชิ้นส่วนและก็จะมีมิติต่างๆ ของโครงข้อแข็งดังในรูปที่แสดง เพื่อนๆ จะเห็นได้ว่าค่าโมดูลัสยืดหยุ่น ค่าพื้นที่หน้าตัดและค่าโมดูลัสความเฉื่อยของทุกๆ ชิ้นส่วนในโครงสร้างชุดนี้จะมีค่าคงที่ทั้งหมด ดังนั้นผมจึงอยากที่จะให้เพื่อนๆ ทุกคนนั้นอาศัยทฤษฎีตามหลักการของ DIRECT STIFFNESS METHOD ในการสร้าง ELEMENT STIFFNESS MATRIX ของชิ้นส่วน AB และ CD เมื่อชิ้นส่วนทั้งสองนี้อ้างอิงไปยัง GLOBAL COORDINATE นะครับ
#โพสต์ของวันเสาร์
#ถามตอบชวนสนุก
#ปัญหาเรื่องการคำนวณหาค่าElementStiffnessMatrixเมื่ออ้างอิงไปยังGlobalCoordinate
เฉลย
ซึ่งหากเพื่อนๆ ติดตามโพสต์ของผมในช่วงสัปดาห์ที่ผ่านมาก็น่าจะเห็นได้ว่าปัญหาข้อนี้นั้นจะมีวิธีในการคำนวณที่มีความซับซ้อนเพิ่มเติมขึ้นมาจากปัญหาในสัปดาห์ที่แล้วแค่นิดหน่อยเท่านั้นเพราะปัญหาในข้อนี้ขอให้เราทำการสร้าง ELEMENT STIFFNESS MATRIX ของชิ้นส่วน AB และ CD เมื่อชิ้นส่วนทั้งสองนี้อ้างอิงไปยัง GLOBAL COORDINATE ซึ่งนั่นก็หมายความว่าจะต้องนำเอามุมของระบบแกนเข้ามามีส่วนเกี่ยวข้องด้วย อีกทั้งหากดูดีๆ จากความสัมพันธ์ของตรีโกณมิติก็จะเห็นได้ว่าชิ้นส่วน AB และ CD นั้นมีขนาดของความยาวที่เท่าๆ กัน นั่นก็คือเท่ากับ 10 เมตร อีกทั้งหากเราทำการตั้งพิกัดจุดเริ่มต้นของชิ้นส่วนทั้งสองให้มีความสอดคล้องซึ่งกันและกันนั่นก็คือ ให้จุด A และ C เป็นพิกัดของ NODE i หรือจุดเริ่มต้นของชิ้นส่วนและก็ให้จุด B และ D นั้นเป็นพิกัดของ NODE j หรือจุดสิ้นสุดของชิ้นส่วน นั่นก็จะส่งผลทำให้เรามีความจำเป็นในการสร้างตัว ELEMENT STIFFNESS MATRIX เพียงแค่เมตริกซ์เดียวก็เป็นอันเรียบร้อยแล้วนั่นเอง เอาเป็นว่าเรามาเริ่มต้นทำการคำนวณกันเลยดีกว่า โดยเริ่มต้นจากการคำนวณหาค่าคงที่ซึ่งจะเป็นค่าสัมประสิทธิ์ของความแข็งเกร็งหรือค่า STIFFNESS COEFFICIENT ของ การเสียรูปเนื่องจากแรงกระทำตามแนวแกน การเสียรูปเนื่องจากแรงดัด และ การเสียรูปเนื่องจากการเคลื่อนที่ในระนาบ กันก่อนนะครับ

K(A) = EA/L
EA/L = [2.50×10^(5)] x [2400] / [10×100]
EA/L = 6×10^(5) KGF/CM
ซึ่งผมก็จะให้ค่าๆ นี้เป็นค่า K1 และ
K(B) = EI/L
EI/L = [2.50×10^(5)] x [1.50×10^(6)] / [10×100]
EI/L = 3.75×10^(8) KGF-CM
ต่อมาก็คือค่าสัมประสิทธิ์ของความแข็งเกร็งค่าต่างๆ โดยเริ่มต้นจาก
12EI/L^(3) = K(B) x 12/L^(2)
12EI/L^(3) = [3.75×10^(8)] x 12/(10×100)^(2)
12EI/L^(3) = 4500 KGF/CM
ซึ่งผมก็จะให้ค่าๆ นี้เป็นค่า K2 ซึ่งต่อมาก็คือ
6EI/L^(2) = K(B) x 6/L
6EI/L^(2) = [3.75×10^(8)] x 6/(10×100)
6EI/L^(2) = 2.25×10^(6) KGF
ซึ่งผมก็จะให้ค่าๆ นี้เป็นค่า K3 ซึ่งต่อมาก็คือ
4EI/L = K(B) x 4
4EI/L = [3.75×10^(8)] x 4
4EI/L = 15×10^(8) KGF-CM
ซึ่งผมก็จะให้ค่าๆ นี้เป็นค่า K4 และค่าสุดท้ายก็คือ
2EI/L = K(B) x 2
2EI/L = [3.75×10^(8)] x 2
2EI/L = 7.5×10^(8) KGF-CM
ซึ่งผมก็จะให้ค่าๆ นี้เป็นค่า K5 และต่อมาก็คือเราจะทำการคำนวณหาค่าคงที่ซึ่งจะเป็นค่าสัมประสิทธิ์ของมุมหรือค่า ALIGNMENT COEFFICIENT ของ ระนาบในการวางตัวของชิ้นส่วน ซึ่งแน่นอนว่ามุม θ ของทั้งส่วนชิ้น AB และ CD นั้นจะมีค่าที่เท่าๆ กันด้วยนะครับ
C = COS(θ)
C = 8 / 10
C = 0.80
ซึ่งผมก็จะให้ค่าๆ นี้เป็นค่า C ซึ่งต่อมาก็คือ
S = SIN(θ)
S = 6 / 10
S = 0.60
ซึ่งผมก็จะให้ค่าๆ นี้เป็นค่า S ซึ่งต่อมาก็คือ
C^(2) = [COS(θ)]^(2)
C^(2) = CC
CC = 0.80^(2)
CC = 0.64
ซึ่งผมก็จะให้ค่าๆ นี้เป็นค่า CC ซึ่งต่อมาก็คือ
S^(2) = [SIN(θ)]^(2)
S^(2) = SS
SS = 0.60^(2)
SS = 0.36
ซึ่งผมก็จะให้ค่าๆ นี้เป็นค่า SS ซึ่งต่อมาก็คือ
CS = [COS(θ)] x [SIN(θ)]
CS = 0.80×0.60
CS = 0.48
ซึ่งผมก็จะให้ค่าๆ นี้เป็นค่า CS และในลำดับต่อมาก็คือ การคำนวณหาค่าสัมประสิทธิ์ต่างๆ ที่จะนำไปใช้สร้าง ELEMENT STIFFNESS MATRIX ของชิ้นส่วน AB และ CD เมื่อชิ้นส่วนทั้งสองนี้อ้างอิงไปยัง GLOBAL COORDINATE นั่นเอง โดยจะเริ่มตั้งแต่ค่าสัมประสิทธิ์ C1 C2 C3 C4 C5 C6 และ C7 ตามลำดับ
C1 = k2 x SS + K1 x CC
C1 = 4500 x 0.36 + 6 x 10^(5) x 0.64
C1 = 385620 KGF/CM
C2 = -k2 x CS + K1 x CS
C2 = -4500 x 0.48 + 6 x 10^(5) x 0.48
C2 = 285840 KGF/CM
C3 = k2 x CC + K1 x SS
C3 = 4500 x 0.64 + 6 x 10^(5) x 0.36
C3 = 218880 KGF/CM
C4 = k3 x S
C4 = 2.25 x 10^(6) x 0.60
C4 = 1350000 KGF/CM
C5 = k3 x C
C5 = 2.25 x 10^(6) x 0.80
C5 = 1800000 KGF/CM
C6 = k4
C6 = 15 x 10^(8)
และ
C7 = k5
C7 = 7.5 x 10^(8)
ดังนั้นเราจึงจะสามารถนำเอาค่าสัมประสิทธิ์ของความแข็งเกร็งต่างๆ ที่คำนวณได้ข้างต้นไปใช้ในการสร้าง ELEMENT STIFFNESS MATRIX ของชิ้นส่วน AB และ CD เมื่อชิ้นส่วนทั้งสองนี้อ้างอิงไปยัง GLOBAL COORDINATE ได้ดังรูปที่ผมนำมาใช้ในการเฉลยปัญหาข้อนี้นั่นเองครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านจากคำตอบในวันนี้น่าที่จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
#โพสต์ของวันอาทิตย์
#ถามตอบชวนสนุก
#ตอบปัญหาเรื่องการคำนวณหาค่าElementStiffnessMatrixเมื่ออ้างอิงไปยังGlobalCoordinate
ADMIN JAMES DEAN
บริษัท ภูมิสยาม ซัพพลาย จำกัด ผู้นำกลุ่มธุรกิจเสาเข็มสปัน ไมโครไพล์ รายแรกและรายเดียวในประเทศไทย ที่ได้การรับรองมาตรฐาน ISO 45001:2018 การจัดการอาชีวอนามัยและความปลอดภัย การให้บริการตอกเสาเข็ม The Provision of Pile Driving Service และได้รับการรับรอง ISO 9001:2015 ของระบบ UKAS และ NAC รายแรกและรายเดียวในประเทศไทย ที่ได้รับการรับรองระบบบริหารงานคุณภาพ ตามมาตรฐานในกระบวนการ การออกแบบเสาเข็มสปันไมโครไพล์ การผลิตเสาเข็มสปันไมโครไพล์ และบริการตอกเสาเข็มเสาเข็มสปันไมโครไพล์ (Design and Manufacturing of Spun Micropile/Micropile and Pile Driving Service) Certified by SGS (Thailand) Ltd.
บริษัท ภูมิสยาม ซัพพลาย จำกัด คือผู้ผลิตรายแรกและรายเดียวในไทย ที่ได้รับการรับรองคุณภาพ Endoresed Brand จาก SCG ด้านการผลิตเสาเข็ม สปันไมโครไพล์ และได้รับเครื่องหมาย มาตรฐาน อุตสาหกรรม มอก. 397-2524 เสาเข็มสปันไมโครไพล์ Spun Micro Pile พร้อมรับประกันผลงาน และความเสียหายที่เกิดจากการติดตั้ง 7+ Year Warranty เสาเข็มมีรูกลมกลวงตรงกลาง การระบายดินทำได้ดี เมื่อตอกแล้วแรงสั่นสะเทือนน้อยมาก จึงไม่กระทบโครงสร้างเดิม หรือพื้นที่ข้างเคียง ไม่ต้องขนดินทิ้ง ตอกถึงชั้นดินดานได้ ด้วยเสาเข็มคุณภาพมาตรฐาน มอก. การผลิตที่ใช้เทคโนโลยีที่ทันสมัย จากประเทศเยอรมัน เสาเข็มสามารถทำงานในที่แคบได้ หน้างานสะอาด ไม่มีดินโคลน เสาเข็มสามารถรับน้ำหนักปลอดภัยได้ 15-50 ตัน/ต้น ขึ้นอยู่กับขนาดเสาเข็มและสภาพชั้นดิน แต่ละพื้นที่ ทดสอบโดย Dynamic Load Test ด้วยคุณภาพและการบริการที่ได้มาตรฐาน เสาเข็มเราจึงเป็นที่นิยมในงานต่อเติม
รายการเสาเข็มภูมิสยาม
1. สี่เหลี่ยม S18x18 cm.
รับน้ำหนัก 15-20 ตัน/ต้น
2. กลม Dia 21 cm.
รับน้ำหนัก 20-25 ตัน/ต้น
3. กลม Dia 25 cm.
รับน้ำหนัก 25-35 ตัน/ต้น
4. กลม Dia 30 cm.
รับน้ำหนัก 30-50 ตัน/ต้น
(การรับน้ำหนักขึ้นอยู่กับสภาพชั้นดินในแต่ละพื้นที่)
☎ สายด่วนภูมิสยาม:
082-790-1447
082-790-1448
082-790-1449
091-947-8945
081-634-6586
🌎 Web:
bhumisiam.com
micro-pile.com
spun-micropile.com
microspunpile.com
bhumisiammicropile.com