สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
หัวข้อในวันนี้จะเกี่ยวข้องกันกับหัวข้อ การคำนวณทางด้านกลศาสตร์โครงสร้าง (STRUCTURAL MECHANICS COMPUTATION หรือ SMC)นะครับ
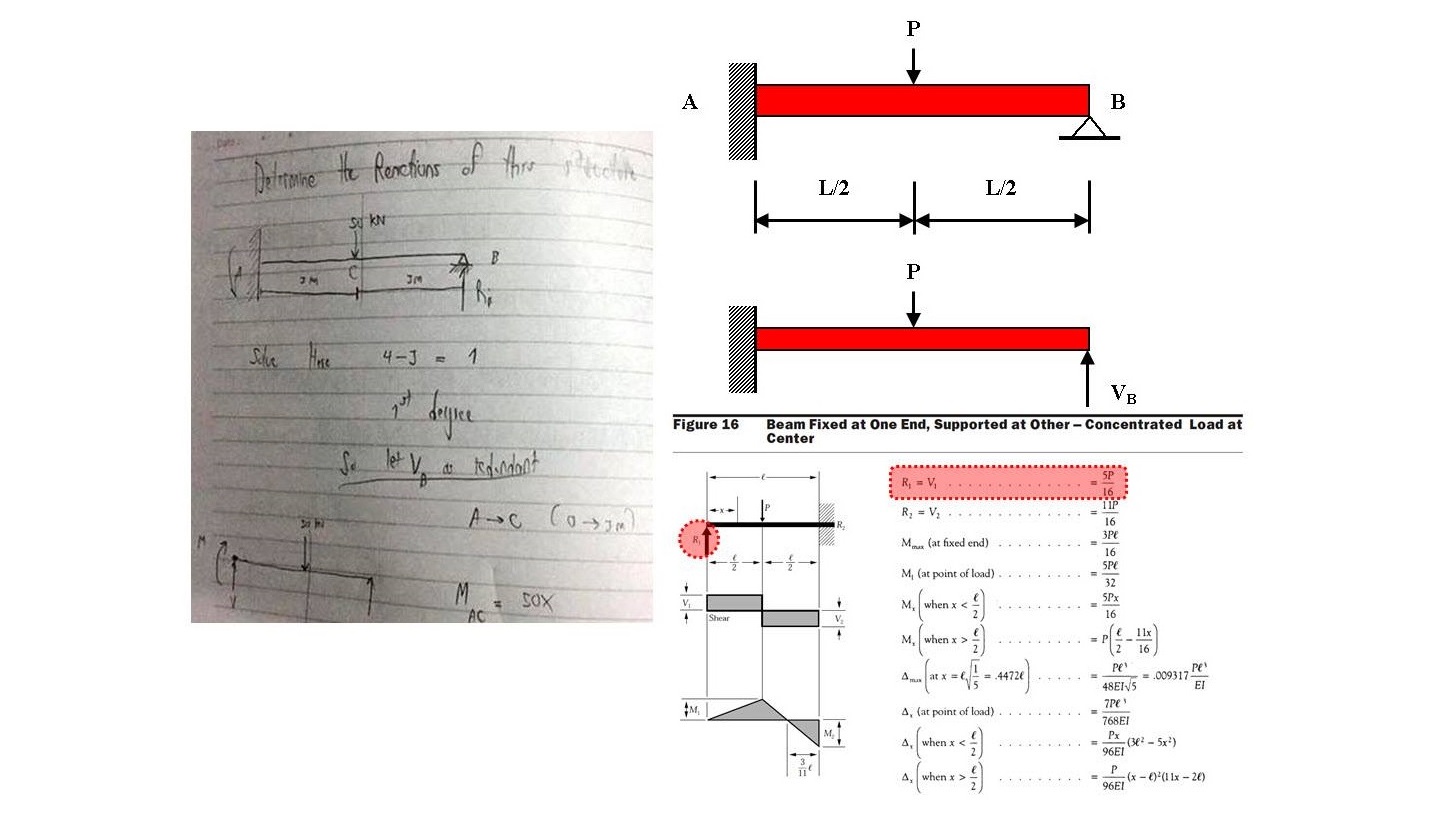
เนื่องจากเมื่อหลายวันก่อนผมได้โพสต์ไปเกี่ยวกับเรื่อง การคำนวณเพื่อวิเคราะห์โครงสร้าง (STRUCTURAL ANALYSIS) เพื่อที่จะหาค่าการเสียรูปที่ปลายของคาน (DISPLACEMENT) โดยในปัญหาข้อนี้ผมใช้ทฤษฎีที่ 2 ของคาสติเกลียโน (CASTIGLIANO’S 2ND THEOREM) วันนี้น้องท่านเดิมได้สอบถามผมมาว่า
“เป็นไปได้หรือไม่ที่จะทำการประยุกต์ใช้วิธีการนี้ในการวิเคราะห์ระบบโครงสร้างที่มีเสถียรภาพ แต่ ไม่สามารถทำการวิเคราะห์ได้ตามหลักการทางสถิตศาสตร์ (STATICALLY INDETERMINATE STRUCTURAL SYSTEM) เหมือนในรูป ตย น่ะครับ ?”
ผมจึงตอบไปว่า ได้แน่นอน เพราะ เราสามารถที่จะนำทฤษฎีที่ 2 ของคาสติเกลียโนนี้มาดัดแปลง และ ประยุกต์ใช้ได้ ซึ่งนั่นก็คือที่มาของ LEAST WORK METHOD นั่นเองนะครับ เรามาดู ตย และ วิธีในการแก้ปัญหาข้อนี้เลยดีกว่านะครับ
เริ่มจากตรวจสอบค่าดัชนีตัวเกิน หรือค่า DI (DEGREE OF INDETERMINACY) ของคานรูปนี้เสียก่อน ซึ่งจะพบว่าเท่ากับ 1 เพราะ ในระบบโครงสร้างจะไม่มีแรงกระทำทางด้านข้าง (LATERAL LOAD) ดังนั้นจึงทำให้ที่ปลายยึดหมุน (HINGED SUPPORT) และ ปลายยึดแน่น (FIXED SUPPORT) จะไม่มีแรงปฏิกิริยาในแนวราบ (LATERAL REACTIONS) เลยนั่นเองครับ
ดังนั้นเราจะทำการกำหนดให้ค่าแรงปฏิกิริยาที่จุด B เป็นค่าแรงตัวเกิน (REDUNDANT) ในระบบโครงสร้างนะครับ
เริ่มจากการตัดช่วงคานตั้งแต่ตำแหน่ง B ถึงตำแหน่งของแรง P เมื่อทำการ INTEGRATE แทนช่วงตั้งแต่ 0 ถึง L/2 เราจะสามารถเขียนสมการโมเมนต์ที่ 1 ออกมาได้เท่ากับ
M(1) = V(B) x
ทำการ PARTIAL DIFFERENTIATE สมการโมเมนต์เทียบกันกับ V(B) จะได้
∂M(1)/∂V(B) = x
ดังนั้นเทอม [M(1)][∂M(1)/∂V(B)] ของช่วงๆ นี้จะมีค่าเท่ากับ
[M(1)][∂M(1)/∂V(B)] = V(B) x^(2)ต่อมาทำการตัดช่วงคานตั้งแต่ตำแหน่งของแรง P ถึงตำแหน่ง A บ้างนะครับ เมื่อทำการ INTEGRATE แทนช่วงตั้งแต่ 0 ถึง L/2 เราจะสามารถเขียนสมการโมเมนต์ที่ 2 ออกมาได้เท่ากับ
M(2) = V(B) (x+L/2) – P x
ทำการ PARTIAL DIFFERENTIATE สมการโมเมนต์เทียบกันกับ V(B) จะได้
∂M(2)/∂V(B) = x+L/2
ดังนั้นเทอม [M(2)][∂M(2)/∂V(B)] ของช่วงๆ นี้จะมีค่าเท่ากับ
[M(2)][∂M(2)/∂V(B)] = V(B) (x+L/2)^(2) – P x (x+L/2)เมื่อตัดสมการโมเมนต์ครบหมดทุกช่วงแล้ว เราก็จะสามารถสร้างสมการการเปลี่ยนรูปร่างที่ตำแหน่งของจุดรองรับ B โดยที่ปัญหาข้อนี้เป็น RIGID SUPPORT ไม่ใช่ FLEXIBLE SUPPORT ซึ่งจะมีค่าเท่ากับ 0 เท่ากับ การรวมผลสมการโมเมนต์ที่ได้รับการ INTEGRATE โดยให้มีช่วงการแทนค่าตามที่ได้ระบุข้างต้นไปได้เท่ากับ
∆(B) = ∑ ∫ [M][∂M/∂V(B)] dx/EI = 0
สำหรับสมการ M(1) เราจะแทนช่วงตั้งแต่ 0→L/2 ดังนั้น
∫ [M(1)][∂M(1)/∂V(B)] dx/EI = 0
∫[V(B) x^(2)] dx/EI = 0
V(B)L^(3)/24 = 0
สำหรับสมการ M(2) เราก็จะแทนช่วงตั้งแต่ 0→L/2 เช่นกัน ดังนั้น
∫ [M(2)][∂M(2)/∂V(B)] dx/EI = 0
∫[V(B) (x+L/2)^(2) – P x (x+L/2)] dx/EI = 0
7V(B)L^(3)/24 – 5PL^(3)/48 = 0
ดังนั้นเทอม
∑ ∫ [M][∂M/∂V(B)] dx/EI = 0
จะมีค่าเท่ากับ
[V(B)L^(3)/24] + [7V(B)L^(3)/24 – 5PL^(3)/48] = 0V(B)L^(3)/3 – 5PL^(3)/48 = 0
V(B)L^(3)/3 = 5PL^(3)/48
V(B) = 5PL^(3)/48 x 3/L^(3)
V(B) = 5P/16
หากเพื่อนๆ ดูในรูปนะครับ ผมได้แนบค่าที่เป็น EXACT SOLUTION เอาไว้ด้วย จะเห็นได้ว่าค่าๆ นี้จะตรงกันนะครับ ดังนั้นหากคานๆ นี้ต้องรับ นน P เท่ากับ 50 kN ก็เท่ากับว่าค่าแรงปฏิกิริยาที่จุดรองรับ B จะมีค่าเท่ากับ
V(B) = 5×50/16 = 15.625 kN
เป็นยังไงบ้างครับ คิดว่าคงไม่ยากจนเกินไปนะครับ อย่าลืมว่าการที่จะเชี่ยวชาญในการวิเคราะห์โครงสร้างโดยวิธีการนี้นอกจากที่จะต้องมีพื้นฐานทางด้านแคลคูลัส (CALCULAS) บ้างแล้ว เรายังจำเป็นที่จะต้องหมั่นฝึกฝนการตัดสมการโมเมนต์รูปแบบต่างๆ ให้ชำนาญอีกด้วยนะครับ ยังไงก็ขอเป็นกำลังใจให้น้องท่านนี้ในการเรียนวิชา STRUCTURAL ANALYSIS โดยเฉพาะเมื่อเลือกใช้วิธี CLASSICAL METHOD อย่าง LEAST WORK METHOD นะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
ADMIN JAMES DEAN
บริษัท ภูมิสยาม ซัพพลาย จำกัด ผู้นำกลุ่มธุรกิจเสาเข็มสปันไมโครไพล์ รายแรกและรายเดียวในประเทศไทย ที่ได้การรับรองมาตรฐาน ISO 45001:2018 การจัดการอาชีวอนามัยและความปลอดภัย การให้บริการตอกเสาเข็ม The Provision of Pile Driving Service และได้รับการรับรอง ISO 9001:2015 ของระบบ UKAS และ NAC รายแรกและรายเดียวในประเทศไทย ที่ได้รับการรับรองระบบบริหารงานคุณภาพ ตามมาตรฐานในกระบวนการ การออกแบบเสาเข็มสปันไมโครไพล์ การผลิตเสาเข็มสปันไมโครไพล์ และบริการตอกเสาเข็มเสาเข็มสปันไมโครไพล์ (Design and Manufacturing of Spun Micropile/Micropile and Pile Driving Service) Certified by SGS (Thailand) Ltd.
บริษัท ภูมิสยาม ซัพพลาย จำกัด คือผู้ผลิตรายแรกและรายเดียวในไทย ที่ได้รับการรับรองคุณภาพ Endoresed Brand จาก SCG ด้านการผลิตเสาเข็ม สปันไมโครไพล์ และได้รับเครื่องหมาย มาตรฐาน อุตสาหกรรม มอก. 397-2524 เสาเข็มสปันไมโครไพล์ Spun Micro Pile พร้อมรับประกันผลงาน และความเสียหายที่เกิดจากการติดตั้ง 7+ Year Warranty เสาเข็มมีรูกลมกลวงตรงกลาง การระบายดินทำได้ดี เมื่อตอกแล้วแรงสั่นสะเทือนน้อยมาก จึงไม่กระทบโครงสร้างเดิม หรือพื้นที่ข้างเคียง ไม่ต้องขนดินทิ้ง ตอกถึงชั้นดินดานได้ ด้วยเสาเข็มคุณภาพมาตรฐาน มอก. การผลิตที่ใช้เทคโนโลยีที่ทันสมัย จากประเทศเยอรมัน เสาเข็มสามารถทำงานในที่แคบได้ หน้างานสะอาด ไม่มีดินโคลน เสาเข็มสามารถรับน้ำหนักปลอดภัยได้ 15-50 ตัน/ต้น ขึ้นอยู่กับขนาดเสาเข็มและสภาพชั้นดิน แต่ละพื้นที่ ทดสอบโดย Dynamic Load Test ด้วยคุณภาพและการบริการที่ได้มาตรฐาน เสาเข็มเราจึงเป็นที่นิยมในงานต่อเติม
รายการเสาเข็มภูมิสยาม
1. สี่เหลี่ยม S18x18 cm.
รับน้ำหนัก 15-20 ตัน/ต้น
2. กลม Dia 21 cm.
รับน้ำหนัก 20-25 ตัน/ต้น
3. กลม Dia 25 cm.
รับน้ำหนัก 25-35 ตัน/ต้น
4. กลม Dia 30 cm.
รับน้ำหนัก 30-50 ตัน/ต้น
(การรับน้ำหนักขึ้นอยู่กับสภาพชั้นดินในแต่ละพื้นที่)
☎ สายด่วนภูมิสยาม:
082-790-1447
082-790-1448
082-790-1449
081-634-6586
🌎 Web:
bhumisiam.com
micro-pile.com
spun-micropile.com
microspunpile.com
bhumisiammicropile.com