การคำนวณหาสถานะของความสมดุล (STAGE OF EQUILIBRIUM)

17352427_1327158863996902_3286763341092713254_n[1]
 

ref:  https://www.facebook.com/bhumisiam/posts/1327158863996902:0

 

 
สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
วันนี้ผมจะขอมายก ตย ในการคำนวณหาสถานะของความสมดุล (STAGE OF EQUILIBRIUM) ในโครงสร้างตามที่ได้เคยรับปากกับเพื่อนๆ เอาไว้เมื่อวานนะครับ
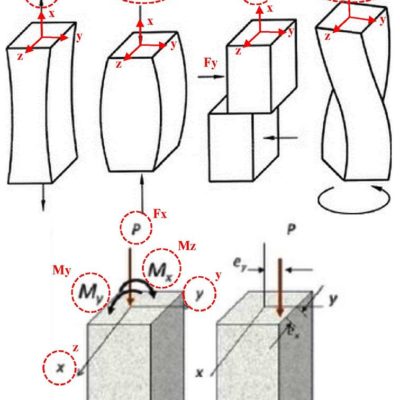
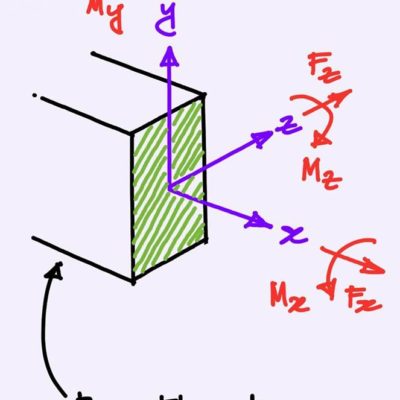
เริ่มต้นดูจากในรูปก่อนนะครับ ในรูปเป็นโครงสร้าง SHELL รูปครึ่งวงกลมวางซ้อนกันอยู่ 2 อัน โดยหากดูรูปในเส้นประสีเขียวจะพบว่า ณ จุดๆ นี้ คือ ตำแหน่งดั้งเดิมของมัน ก่อนที่จะเกิดการหมุนตัวไปเท่ากับมุม θ ซึ่งหมายความว่าหากก่อนการหมุนค่ามุม θ จะเท่ากับ 0 ดังนั้นหากไม่มีแรงกระทำใดๆ มาผลักหรือหมุน SHELL นี้ สภาวะของความสมดุลของ SHELL นี้ก็จะอยู่ในสภาวะที่เรียกว่าสมดุลสะเทิน หรือ ผลจากการ PARTIAL DIFFERENTIATE ไม่ว่าจะสักกี่ ORDER ก็ตามก็จะออกมาเท่ากับ 0 หรืออาจเขียนได้ว่า
∂^(n)V / ∂θ^(n) = …… = ∂^(∞)V / ∂θ^(∞) = 0 (เมื่อแทนค่าให้ θ = 0)
มาดูกันต่อนะครับ ก่อนการหมุนระยะในสมการ y จะมีค่าเท่ากับ
y = 2r – r/2 = 3r/2
แต่เมื่อใดก็ตามที่เกิดการหมุนจนทำให้เกิดมุม θ นั้นเกิดขึ้นในตัว SHELL นี้จะพบว่าระยะในสมการ y จะลดลงไปจากเดิมเป็น
y = 2 r cos (θ) – r/2 cos (2θ)
ซึ่งในสมการๆ นี้ค่า θ ก็คือตัวแปรที่เราให้เป็น GENERALIZED COORDINATE นั่นเองครับ
มาเริ่มต้น PARTIAL DIFFERENTIATE กันใน 1ST ORDER กันนะครับ
∂V / ∂θ = -2 r sin (θ) + r sin (2θ) = 0
ต่อด้วยการ PARTIAL DIFFERENTIATE กันใน 2ND ORDER กันนะครับ
∂^(2)V / ∂θ^(2) = -2 r cos (θ) + 2 r cos (2θ) = 0
ในขั้นตอนนี้เองครับ หากเรา SET คำตอบของสมการให้เท่ากับ 0 เราจะสามารถแก้สมการหาคำตอบของตัวแปร GENERALIZED COORDINATE ที่จะทำให้โครงสร้างนี้สมดุลได้นั่นเอง
โดยหากเพื่อนๆ ลองแก้สมการเหล่านี้ดูจะพบว่าค่า θ ทีไ่ด้ออกมานั้นจะมีหลายคำตอบมาก ซึ่งแน่นอนที่สุดเราจะเลือกค่าของคำตอบที่มีค่าน้อยที่สุดเพื่อเป็นคำตอบของมุม θ ที่สามารถเกิดขึ้นได้ในโครงสร้างของเรา
ต่อด้วยการ PARTIAL DIFFERENTIATE กันใน 3RD ORDER กันนะครับ
∂^(3)V / ∂θ^(3) = 2 r sin (θ) – 4 r sin (2θ) = 0 (เมื่อแทนค่าให้ θ = 0)
ต่อด้วยการ PARTIAL DIFFERENTIATE กันใน 4TH ORDER กันนะครับ
∂^(4)V / ∂θ^(4) = 2 r cos (θ) – 8 r cos (2θ) = -6r < 0 (เมื่อแทนค่าให้ θ = 0) เพื่อนๆ เห็นคำตอบในการ PARTIAL DERIVATIVE นี้ใช่มั้ยครับ คำตอบที่ออกมามีค่าเท่ากับ -6r ซึ่งจะน้อยกว่า 0 ดังนั้นโครงสร้าง SHELL เมื่อต้องวางตัวอยู่ในระนาบมุม θ ใดๆ ถึงจะทำให้มุมๆ นี้อยู่ในค่าๆ หนึ่งที่จะทำให้โครงสร้างทั้งระบบอยู่ในสมดุล (EQUILIBRIUM) ได้ แต่ สถานะของความสมดุล (EQUILIBRIUM STAGE) นี้ก็ยังถือว่าเป็นแบบไม่เสถียร (UNSTABLE) อยู่ดีครับ ก็หวังว่าเพื่อนๆ จะพอเข้าใจถึงการนำหลักการ ENERGY METHODS ที่ผมนำมาเล่านี้ไปใช้ในการประยุกต์ในการตรวจสอบสถานะของความสมดุลในโครงสร้างที่เพื่อนๆ อาจจะต้องมีส่วนเกี่ยวข้องอยู่ได้นะครับ หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย จนกว่าจะพบกันใหม่นะครับ ADMIN JAMES DEAN BSP-Bhumisiam คุณภาพทีมงานช่างมาตรฐาน คุณภาพเครื่องจักรมาตรฐาน งานเอกสารตรวจสอบเชื่อถือได้ คุณภาพเสาเข็มมาตรฐาน มอก. 397-2524 เสาเข็ม สปันไมโครไพล์ ช่วยแก้ปัญหาได้เพราะ 1) สามารถทำงานในที่แคบได้ 2) ไม่ก่อให้เกิดมลภาวะทางเสียง 3) หน้างานสะอาด ไม่มีดินโคลน 4) สามารถรับน้ำหนักได้ 20-40 ตัน/ต้น 5) สามารถตอกชิดผนังกำแพง ไม่ทำให้โครงสร้างเดิมเสียหาย สนใจติดต่อสินค้า เสาเข็ม ไมโครไพล์ (Micropile) สปันไมโครไพล์ (Spun MicroPile) มาตรฐาน มอก. ติดต่อ สายด่วน โทร : 081-634-6586 082-790-1447 082-790-1448 082-790-1449 ติดต่อ สายด่วน โทร 081-634-6586 http://www.micro-pile.com