สวัสดีครับแฟนเพจที่รักทุกท่าน
เรื่องที่จะนำมาเล่าสู่กันฟังในวันนี้ก็คือ ค่าโมดูลัสยืดหยุ่นระยะยาวในคอนกรีตทั่วๆ ไป หรือ LONG TERM MODULUS OF ELASTICITY IN NORMAL CONCRETE นั่นเองครับ

(รูปที่ 1)
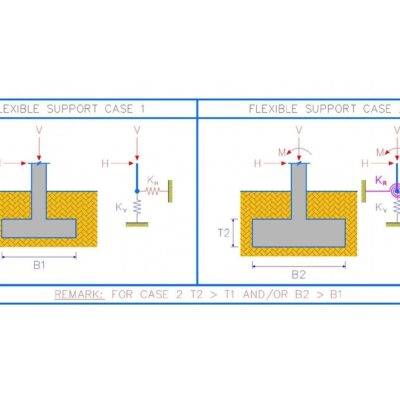
ก่อนอื่นผมต้องขอท้าวความก่อนนะครับว่าเวลาที่ผมพิจารณาออกแบบโครงสร้าง คสล ที่มีความยาวช่วงมากๆ ที่มีการรับ นน แบบคงค้างเป็นระยะเวลายาวนาน ดังนั้นจึงจำเป็นจะต้องพิจารณาสภาวะการโก่งตัวทั้งในสภาวะอันสั้น (SHORT TERM DISPLACEMENT) และสภาวะยาวนาน (LONG TERM DISPLACEMENT) ด้วย ซึ่งอีกเช่นเคยครับ ผมอ้างอิงจากมาตรฐานฝั่งอังกฤษเป็นหลัก ซึ่งก็คือ BS CODE (ดูรูปที่ 1) โดยที่ผมจะต้องคำนึงถึงค่าๆ นี้เสมอ เพื่อนทราบหรือไม่ครับว่าเพราะอะไร ?

(รูปที่ 2)
หากเราพิจาณาโครงสร้าง คสล ที่ต้องรับ นน บรรทุกคงค้างเราต้องไม่ลืมว่าจะเกิดพฤติกรรมหนึ่งขึ้นในวัสดุคอนกรีตซึ่งถือเป็นพฤติกรรมที่ค่อนข้างมีความซับซ้อนมากพฤติกรรมหนึ่งของวัสดุคอนกรีต นั่นก็คือ การคืบตามกาลเวลา (CREEP) ดังนั้นที่สภาวะนี้คอนกรีตจะมีค่าการเสียรูปเนื่องจากการหดตัวที่สูงขึ้นมากๆ หรือ พูดภาษาชาวบ้านๆ ก็คือ คอนกรีตจะมีความอ่อนตัวลงเมื่อทำการเปรียบเทียบค่าๆ นี้กับในช่วงแรกๆ ที่ทำการหล่อคอนกรีตขึ้นมา (ดูรูปที่ 2) ซึ่งก็คือช่วงที่เราใช้ในการคำนวณค่าโมดูลัสยืดหยุ่นของคอนกรีตทั่วๆ ไป ซึ่งที่สภาวะแรกเริ่มนี้ค่าโมดูลสัสยืดหยุ่นของคอนกรีตจะมีค่าเท่ากับค่าโมดูลัสยืดหยุ่นระยะสั้นของคอนกรีตซึ่งมีค่าเท่ากับ
Ec = 15100√(fc’) (1)
เราจะเห็นได้จากในรูปที่ (2) ว่าเมื่อเวลาผ่านไป ค่ากำลังอัดของคอนกรีตจะยังคงเท่าเดิมแต่สิ่งที่เปลี่ยนไปก็คือค่าการเสียรูปที่สูงขึ้นมากอันเนื่องจากผลของการคืบที่เกิดขึ้นตามระยะเวลาที่ยาวนานขึ้นนั่นเอง และ เมื่อความชันของเส้นโค้งความสัมพันธ์ระหว่างค่าความเค้นและความเครียดนี้มีค่าลดลงก็จะทำให้ค่าโมดูลัสยืดหยุ่นในช่วงนี้มีค่าที่ลดลงไปด้วย หรือ ที่เราเรียกว่าค่าโมดูลัสยืดหยุ่นระยะยาวของโครงสร้างนั่นเอง

(รูปที่ 3)
ดังนั้นหากเราให้ค่าโมดูลัสยืดหยุ่นระยะยาวของคอนกรีตมีค่าเท่ากับ Ec’ แล้วจะพบได้ว่า Ec’ จะมีค่าน้อยกว่าค่า Ec ที่คำนวณได้จากในสมการที่ (1) เสมอ โดยหากเราทราบว่าค่าโมดูลัสยืดหยุ่นระยะสั้นนั้นจะมีค่าเท่ากับค่าความเค้นช่วงยืดหยุ่นต่อค่าความเครียดช่วงยืดหยุ่น (ดูรูปที่ 3) เราจึงสามารถแทนค่าสมการที่ (1) ใหม่ได้เป็น
Ec = σc / εc = fc / εc (2)
โดยหากเราพิจารณาในระยะเวลาอันยาวนานแล้วและให้ค่าแฟคเตอร์ของการคืบในคอนกรีตมีค่าเท่ากับ Ø เมื่อเวลาผ่านไปนานเข้า จะทำให้ค่าการหดตัวเพิ่มขึ้นเป็นอัตราส่วนตรงกับค่า Ø นี้ ดังนั้นค่า εc ในสมการที่ (2) นี้จะต้องเปลี่ยนเป็น (Ø)(εc) ดังนั้นหากให้ค่า εc’ เป็นค่าความเครียดระยะยาว เราสามารถเขียนค่าๆ นี้ให้มีค่าเท่ากับ
εc’ = εc + Øεc = εc(1+Ø) (3)
ดังนั้นหากแทนค่าในสมการที่ (3) ลงในสมการที่ (2) จะได้ค่าโมดูลัสยืดหยุ่นระยะยาวมีค่าเท่ากับ
Ec’ = σc / εc = fc / εc(1+Ø) = Ec/(1+Ø) (4)
จะเห็นได้จากในสมการที่ (4) ว่าค่าโมดูลัสยืดหยุ่นระยะยาว Ec’ จะมีค่าน้อยกว่าค่าโมดูลัสยืดหยุ่นระยะสั้นเสมอ โดยน้อยกว่ามีค่าเท่ากับเป็นสัดส่วนต่อค่า (1+Ø)
หากทำการ
สมมติให้ค่า Ø มีค่าเท่ากับ 2.00 ดังนั้นค่า
Ec’ = Ec/(1+2) = Ec/3
จะเห็นได้ว่าค่าโมดูลัสยืดหยุ่นระยะยาวจะมีค่าน้อยกว่าค่าโมดูลัสยืดหยุ่นระยะสั้นอยู่ที่ประมาณ 3 เท่า เมื่อเป็นเช่นนี้เวลาที่เพื่อนๆ ต้องทำการออกแบบสภาวะการใช้งานของโครงสร้าง คสล ที่ต้องรับ นน บรรทุกคงค้างเป็นระยะเวลานานๆ ก็อย่าลืมพิจาณาเรื่องโมดูลัสยืดหยุ่นระยะยาวของคอนกรีตซึ่งจะเกิดจากผลของการคืบนี้ด้วยนะครับ
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากพี่แขก และ เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
ADMIN JAMES DEAN