สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
วันนี้ผมจะมาขอยก ตย ความรู้พื้นฐานที่เราควรจะทราบที่มาที่ไปของสมการที่เราใช้งานกันบ่อยๆ แต่อาจจะหลงลืมไปกันไปบ้างต่อนะครับ
หลังจากเมื่อ 2 วันที่ผ่านมาผมยก ตย ถึงสมการทางด้านกลศาสตร์ของวัสดุไปบ้างแล้ว วันนี้ผมจะขอยก ตย ถึงสมการทางด้านการออกแบบบ้างนะครับ
สมการที่เกี่ยวข้องกับงานออกแบบที่ผมต้องการจะหยิบยกมาในวันนี้เกี่ยวข้องกับการออกแบบหน้าตัดโครงสร้าง คสล ที่ต้องรับแรงดัดโดยวิธีหน่วยแรงใช้งานนะครับ
เราอาจคุ้นเคยกันดีถึงสมการเหล่านี้
k = 1/( 1 + fs / n fc ) (1)
j = 1 – k / 3 (2)
Mc = 1/2 fc j k b d^(2) (3)
As = M / fs j d (4)
ผมก็เชื่อเหลือเกินว่าหากสอบถามเพื่อนๆ ถึงที่มาของสมการเหล่านี้ เพื่อนๆ บางคนอาจตอบได้นะครับ แต่โดยมากก็อาจจะตอบผมไม่ได้ว่าวิธีและกระบวนการในการหาสมการเหล่านี้นั้นมีที่มาที่ไปอย่างไร วันนี้เราจะมาทบทวนกันดูนะครับ
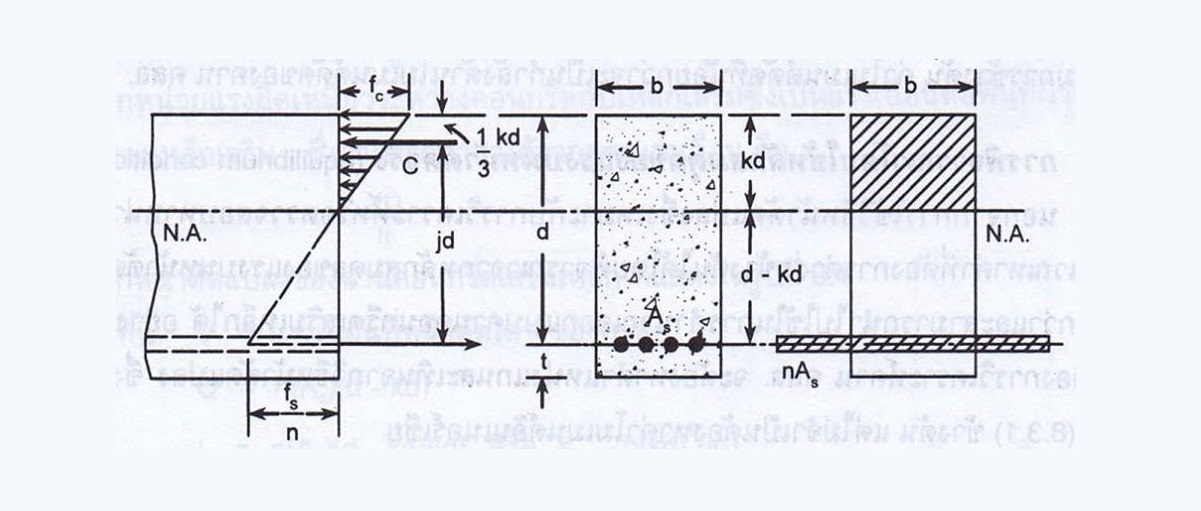
ดูรูปที่แนบมานะครับ พิจารณารูปย่อยทางด้านซ้ายมือสุดนะครับ คานเป็นแบบช่วงเดียว วางอยู่บนฐานที่เป็นจุดหมุนทั้งสองข้าง เนื่องจากคานนี้ต้องรับ นน บรรทุกที่กระทำบนคานจึงทำให้เกิดแรงภายในที่เป็นค่าโมเมนต์ขึ้นในคานมีค่าเท่ากับ M โดยจะดัดทำให้คานแอ่นตัวลง หรือ ที่เราเรียกว่าการดัดแบบโมเมนต์มีค่าเป็นบวกกระทำบนหน้าตัดของคาน ในการที่หน้าตัดนี้จะสมดุลได้จำเป็นจะต้องมีแรงภายในที่ต้านทานต่อค่าโมเมนต์บวก หรือค่า M นี้ นั่นก็คือแรงอัดหรือแรง C ที่ผิวด้านบนของคานและแรงดึง T ที่ผิวด้านล่างของคาน โดยที่ระยะห่างระหว่างแรง C และ T นั้นเราจะให้มีค่าเท่ากับระยะ j d เมื่อค่า d คือความความลึกประสิทธิผลของหน้าตัด หรือ คือระยะห่างระหว่างผิวที่รับหน่วยแรงอัดสูงสุดไปจนถึงเซ็นทรอยด์ของเหล็กเสริมนั่นเอง โดยที่หน้าตัดนี้เป็นรูปสี่เหลี่ยมผืนผ้าความกว้างเท่ากับ b ดังนั้นการกระจายตัวของหน่วยแรงอัดในคอนกรีตจะกระทำเป็นรูปทรงสามเหลี่ยม เราจะให้ฐานของสามเหลี่ยมนี้มีค่าเท่ากับระยะ k d ดังนั้นแรง C จะกระทำผ่านเซ็นทรอยด์ของรูปสามเหลี่ยมนี้ คือ k d / 3 วัดจากผิวด้านบนสุดของคาน ดังนั้นเราจะทราบว่าค่าโมเมนต์จะมีค่าเท่ากับแรงคูณกับแขนของแรง หรือ เท่ากับ
M = C j d = T j d
โดยหากเราพิจารณาในสภาวะที่ยังเป็นเชิงเส้นอยู่ เมื่อค่าหน่วยการหดตัว εc ของคอนกรีต และ หน่วยการยืดตัว εs ของเหล็ก เราจะอาศัยหลักการทางด้านกลศาสตร์ที่ว่าค่าหน่วยแรงสูงสุดของวัสดุใดๆ จะมีค่าเท่ากับหน่วยการยืดหรือหดตัวของวัสดุนั้นๆ คูณกับค่าโมดูลัสยืดหยุ่นของวัสดุนั้นๆ หรือค่า f = ε E ดังนั้น
fc = εc Ec
และ
fs = εs Es
หากเราใช้หลักการของสามเหลี่ยมคล้ายเราจะสามารถสร้างความสัมพันธ์ได้ว่า
εc/εs = (fc/Ec)/(Es/fs) = fc Es / fs Ec
หากค่า n คือค่า MODULAR RATIO = Es/Ec ดังนั้น
n fc / fs = kd / (d – kd)
จะเห็นได้ว่าเราสามารถดึง d ซึ่งเป็นตัวร่วมออกได้ สมการข้างต้นจะกลายเป็น
n fc / fs = k / ( 1 – k )
ทำการแก้สมการออกมาจะได้ที่มาของสมการที่ (1) ว่า
k = 1/( 1 + fs / n fc )
เมื่อเราทราบว่าแขนของแรง C และ T มีค่าเท่ากับ jd และตำแหน่งของแรง C จะกระทำผ่านเซ็นทรอยด์ของรูปสามเหลี่ยมเท่ากับระยะ k d / 3 ดังนั้น
jd = d – kd/3
จะสังเหตเห็นได้ว่าเราสามารถดึง d ซึ่งเป็นตัวร่วมออกได้ สมการข้างต้นจึงกลายเป็นที่มาของสมการที่ (2)
j = 1 – k /3
ต่อมาหากเราต้องการจะคำนวณหาแรง C เราก็สามารถคำนวณ พท ของหน่วยแรงในคอนกรีตได้ว่า
C = 1/2 x สูง x ฐาน x ความกว้าง = 1/2 fc kd b
เมื่อคูณค่า C เข้ากับแขนของแรง jd จะได้ค่าโมเมนต์สูงสุดที่คอนกรีตสามารถจะรับได้ ซึ่งเป็นที่มาของสมการที่ (3) ว่า
Mc = 1/2 fc j k b d^(2)
ในอีกทางหนึ่งหากเราต้องการจะคำนวณหาแรง T เราก็สมารถคำนวณได้ง่ายๆ จาก พท ของเหล็กเสริมคูณกับหน่วยแรงของเหล็กเสริมได้ว่า
T = As fs
เมื่อคูณค่า T เข้ากับแขนของแรง jd จะได้ค่าโมเมนต์สูงสุดที่เหล็กสมารถจะสามารถรับได้ว่า
Ms = As fs j d
ดังนั้นหากเราแทนค่า Ms ด้วย M ใดๆ เราก็จะสามารถหาค่า พท หน้าตัดของเหล็กเสริมได้จากสมการๆ นี้ซึ่งท้ายที่สุดแล้วก็จะเป็นที่มาของสมการที่ (4) ว่า
As = M / fs j d
โอกาสหน้าผมจะมาอธิบายต่อนะครับว่าเหตุใดเราจึงควรม่ีความเข้าใจถึงที่มาที่ไปของสมการเหล่านี้
หวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากพี่แขก และ เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
ADMIN JAMES DEAN